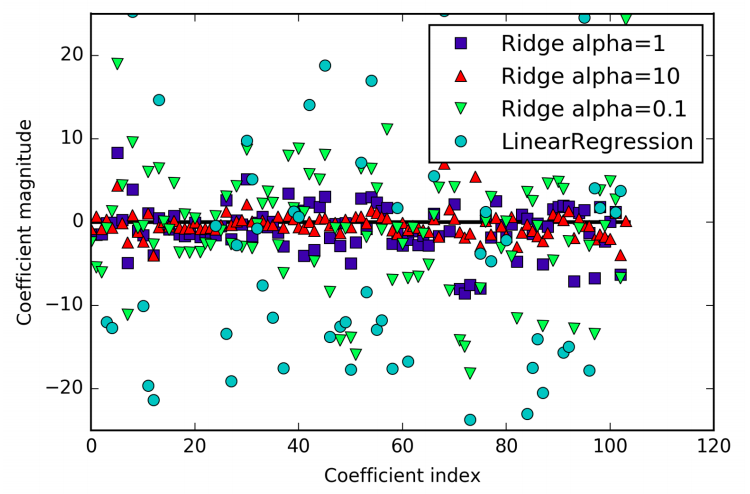
Ridge is also a linear model for regression, so the formula it uses to make predictions is the same one used for ordinary least squares. In ridge regression, thought, the coefficients \(\Theta\) are chosen not only so that they predict well on the training data, but also to fit an additional constraint. We also want the magnitude of coefficients to be as small as possible; in other words, all entries of \(\Theta\) should be close to 0. Intuitively, this means each feature should have as little effect on the outcome as possible (which translates to having a small slope), while still predicting well. This constraint is an example of what is called regularization. Regularization means explicitly restricting a model to avoid overfitting. The particular kind used by ridge regression is known as L2 regularization.
In:
from sklearn.linear_model import Ridge
ridge = Ridge().fit(X_train, y_train)
print("Training set score: {:.2f}".format(ridge.score(X_train, y_train)))
print("Test set score: {:.2f}".format(ridge.score(X_test, y_test)))
Out:
Training set score: 0.89
Test set score: 0.75
Ridge is a more restricted model, so we are less likely to overfit. A less complex model means worse performance on the training set, but better generalization. The Ridge model makes a trade-off between the simplicity of the model (near-zero coefficients) and its performance on the training set. How much importance the model places on simplicity versus training set performance can be specified by the user, using the alpha parameter. In the previous example, we used the default parameter alpha=1.0. The optimum setting of alpha depends on the particular dataset we are using. Increasing alpha forces coefficients to move more toward zero, which decreases training set performance but might help generalization. A higher alpha means a more restricted model.